The Beauty of Uniform Distribution Modulo One
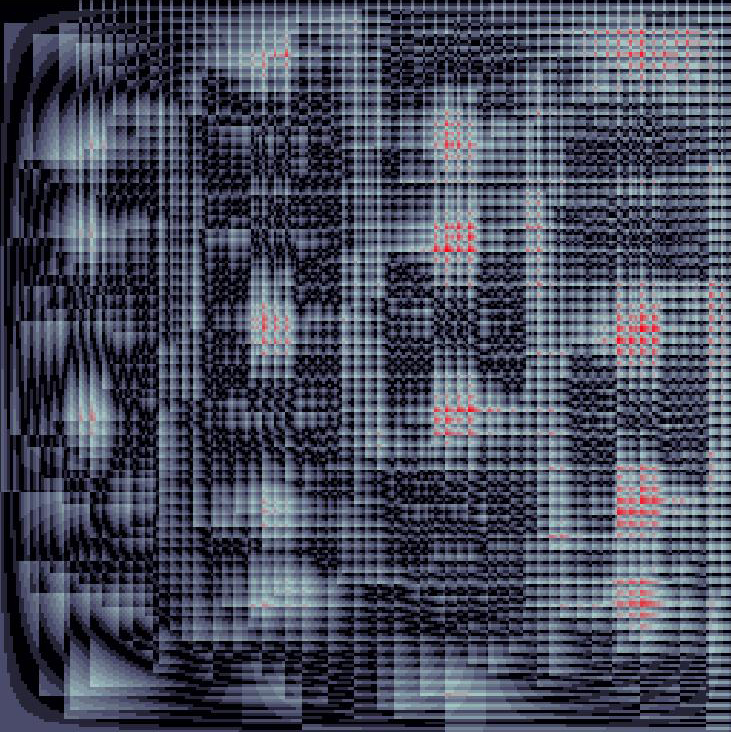
The figures visualize local discrepancy of special point sets in the unit square. Discrepancy is a classical measure of the theory of uniform distribution modulo one. It determines the quality of equidistiribution.
The theory of uniform distribution deals with - nomen est omen - uniformly distributed point sets and sequences. It includes extensive developments within and among several mathematical disciplines and numerous applications, mostly in the fields of Monte-Carlo- and quasi-Monte Carlo Methods (including areas like numerical integration, random number generation, stochastic simulation and approximation theory).
Using such graphical representations of (local) discrepancy, I want to demonstrate my understanding of the "beauty" of this theory.
For some details follow the links
- K. Entacher. On the Beauty of Uniform Distribution Modulo One. The Mathematica Journal, volume 9 (3), 2005.
- K. Entacher Schöne Theorie der Gleichverteilung. NOEO Wissenschaftsmagazin Salzburger Bildungs- und Forschungseinrichtungen, Ausgabe 01/2001 (article.zip)
- K. Entacher. Discrepancy Estimates Based on Haar Functions. Mathematics and Computers in Simulation, 55, 49--57, 2001 (article.pdf).
Images
NAWI:
Two large (1x1m) printouts of local-discrepancy are situated at the Naturwissenschaftlichen Fakultät, University Salzburg, at the entrances of the blue and green lecture rooms.


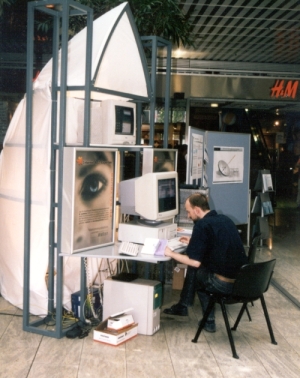
SCIENCEWEEK:
Presentation of large printouts of local-discrepancy visualizations at ScienceWeek2001 (copy of the original ScienceWeek program in German):
Schöne neue Mathematik
Beschreibung: Schöne "neue" Mathematik!(Veranstaltungsnummer: 1588)
Mathematik ist nicht gleich Mathematik. Durch die Verwendung von Computern hat sich dieses Gebiet in den letzten 20 Jahren gewaltig verändert. Diese technische Hilfe bietet nicht nur neue Methoden um mathematische Probleme zu lösen sondern ermöglicht es auch schwierige Theorien und Formeln visuell so darzustellen, dass Mathematik zum staunen und angreifen wird. Wir verbinden wir Wissenschaft mit Kunst: großflächige mathematische Bilder im Einkaufszentrum und deren verständliche Erklärung entführen den Laien in die Welt der schönen Mathematik.
Veranstalter:
FH Studiengang TKS/FH-Salzburg GmbH und
Institut für Scientific Computing/ Universität Salzburg
Schillerstrasse 30
5020 Salzburg
Homepages: http://www.fh-salzburg.ac.at and http://www.cosy.sbg.ac.at/
Veranstaltungsadresse: Europark Salzburg, Klessheim, 5020 Salzburg