Wie kam der Zufall in den Computer?

Die Lehmer's in Berkeley

Dies ist eine kurze Geschichte einer außergewöhnlichen Wissenschafterfamilie und der Entwicklung eines Algorithmus zur Erzeugung von Zufallszahlen sowie dessen, in Folge der Weiterentwicklung, unsachgemäßer Implementierung. Der genannte Algorithmus hat den Weg in eine Fülle von Anwendung gefunden, vom Einarmigen Banditen bis zu Microsoft Excel lässt sich die Palette der Einsätze beschreiben. Diese einfache Idee zeigt aber auch, wie wichtig eine fundamentale Ausbildung in der Informatik ist, und wie es ohne fundiertes Grundlagenwissen in der Folge zu fatalen Fehlern kommen kann.

Wir beginnen in den USA an der University of California in Berkeley. Dort arbeiteten und forschten Derrik Norman Lehmer (1867-1938), sein Sohn Derrik Henry Lehmer (1905-1991) und dessen Frau Emma Trotskaia Lehmer (1906-). Alle drei waren sie Spezialisten in einer mathematischen Disziplin, der Zahlentheorie, genannt “die Königin der Mathematik”.

Derrik Norman Lehmer Derrik Henry Lehmer Emma Trotskaia Lehmer

Derrik N. Lehmer beschäftigte sich intensiv mit der Fragestellung der Faktorisierung von Zahlen. Faktorisierung bedeutet die Zerlegung von ganzen Zahlen in ein eindeutig gegebenes Produkt von Primzahlen. Hier ein einfaches Beispiel: Die Zahl 12 lässt sich in eindeutiger Weise als Produkt der ersten beiden Primzahlen 2 und 3 darstellen, nämlich 12 = 2 . 2 . 3 = 22 . 3. Etwas komplizierter, die Zahl 234234 lässt sich durch die Primzahlen 2, 3, 7, 11 und 13 faktorisieren, und zwar 234234 = 2 . 32 . 7 . 11 . 132. Die Primzahlen sind hierbei die Bausteine aus denen sich jede beliebige Zahl in Form eines Produktes darstellen lässt. Eine Primzahl selbst ist nicht mehr teilbar oder gleichbedeutend damit, nicht mehr als Produkt von ganzen Zahlen darstellbar. Es ist im Allgemeinen sehr schwierig so eine Faktor - Zerlegung von sehr großen Zahlen anzugeben, zum Beispiel einer Zahl mit 500 Dezimalstellen. In ähnlicher Weise ist es sehr schwer nachzuweisen ob eine große Zahl eine Primzahl ist oder nicht. Die Problematik der Faktorisierung wurde viel später, erst in den vergangenen Jahren sehr populär, da man die Schwierigkeit der Zerlegung großer Zahlen in Produkte ausgenutzt hat um geeignete Verfahren zur Verschlüsselung von Informationen zu entwickeln. Ein Beispiel dafür ist der RSA Algorithmus (siehe Links).

Das Bild oben zeigt ein Resultat von Lehmer’s Arbeit und zwar die Publikation von Faktor-Tabellen der ersten 10 Millionen Zahlen (Carnegie Institution of Washington, 1909). Dies war in der damaligen Zeit nicht ganz so einfach wie im Computerzeitalter heute, wie man vielleicht aus dem im Folgenden abgebildeten Auszug eines „händisch“ gerechneten Nachweises einer Primzahleigenschaft seines Sohnes aus dem Jahr 1932 vermuten kann.

D.N.Lehmer war neben seiner akademischen Karriere begeisterter Musiker und Poet. Er veröffentlichte neben vielen Liedern drei größere musikalische Werke (zwei davon Opern) und mehrere Gedichtbände. Er war auch wesentlicher Förderer der Karriere seines Sohnes D.H.Lehmer welcher durch seinen Vater auch dessen Studentin Emma Trotskaia, seine spätere Frau, kennen gelernt hat.

D.H.Lehmer beschäftigte sich wie sein Vater mit zahlentheoretischen Fragestellungen. Er entwickelte sich zu einer führenden Autorität in der Zahlentheorie und folglich auch in der sich damals rasch entwickelnden Computerwissen-schaft. Neben persönlichen wissenschaftlichen Interessen bearbeiteten die drei Lehmer‘s auch viele gemeinsame Fragestellungen als Beispiel seien wichtige Beiträge zur Erforschung des berühmten Problems von Fermat: „Fermat‘s Letztem Satz“ erwähnt, welcher nach 350 ungelösten Jahren, erst im Jahre 1993 durch Andrew Wiles gelöst wurde (siehe Links).

Ein weiterer wissenschaftlicher Erfolg der Lehmer‘s war die Entwicklung von elektromechanischen Maschinen zur Faktorisierung von Zahlen (siehe Bilder unten). D.H.Lehmer entwickelte verschiedenste Verfahren basierend auf Fahrradketten, Filmspulen, Zahnrädern in Kombination mit elektronischem Antrieb und Steuerung um geeignete Faktoren von großen Zahlen zu finden.

Die Funktionsweise dieser Maschinen beruht auf einem bereits sehr alten mathematischen Prinzip des Griechen Eratosthenes um 230 v.Chr. Erwähnenswert dabei ist, dass die erste mechanische Realisierung dieser Methode von einem Österreicher namens Anton Felkel stammt, welcher im Jahre 1776 mit Hilfe seines Verfahren eine Faktorentabelle bis zur Zahl 408.000 publizierte. Aber dies ist eine andere spannende Geschichte (siehe Links).

D.H. Lehmer war in den folgenden Jahren (~1945-1955) wesentlich an der Entwicklung der ENIAC (Electronic Numeric Integrator and Calculator), einer der ersten sehr großen Rechenmaschinen (siehe Info-Box) beteiligt. ENIAC rechnete nicht wie heutige Computer mit Binärzahlen sondern im Dezimalsystem und wurde hauptsächlich für physikalische Berechnungen und Simulationen verwendet. Speziell für diese Maschine hat D.H.Lehmer einen einfachen arithmetischen Algorithmus zur Erzeugung von Zufallszahlen vorgeschlagen welche als Basis für Simulationen benötigt wurden. Die Idee dieses Algorithmus ist unmittelbar mit Lehmer‘s zahlentheoretischer Erfahrung verbunden. Lehmer‘s Zufallsgenerator funktioniert in der ursprünglichen Version folgendermaßen: Wir betrachten die Zahlen n=1,2,3,... und berechnen dazu die Potenzen an, wobei a = 23. Als „Zufallszahl“ wird der Rest xn verwendet der bei Division von an durch m = 108+1 = 100000001. entsteht. Somit erhält man eine Folge von „Resten“ kleiner m. Dividiert man diese Folge von Zahlen durch den „Modul“ m, dann erhält man Werte un = xn / m die zwischen 0 und 1 liegen und in ihrem Verhalten sehr zufällig, und zwischen 0 und 1 gleichmäßig verteilt erscheinen (siehe Info-Box).

Zitat (Math. Rev. 1952): By repeating this process he (D.H. Lehmer) generates a sequence un which he shows has a repetition period of 5.882.352 (= (108+1)/17 – 1). An IBM 602A was used to generate 5000 numbers of such a sequence. Four standard tests (unspecified) were applied to check the „randomness“, and the sequence passed all four. The author observes, however, that all of the members of the sequence he chose were divisible by 17.

Dieser Algorithmus, genannt der Lineare Kongruenzgenerator, wurde im Laufe der Zeit weiterentwickelt und modernisiert. Dabei waren D.H.Lehmer und viele weitere namhafte Mathematiker und Informatiker beteiligt unter anderem auch Donald Knuth der „Papst der Informatik“. Es wurden wichtige Grundvoraussetzungen für die Zahlen die diesen Zufallszahlengenerator definieren festgelegt. Um ein Beispiel zu nennen: einer der am weitesten verbreiteten Generatoren ist definiert durch die Zahlen a = 75 = 16807 und m = 231-1 welche den Algorithmus wie beim Ursprungsgenerator von Lehmer definieren. Die Zahlen a und m haben in diesem Fall besondere Eigenschaften, und zwar ist m ist eine Primzahl welche in einem 32-bit Computer als Integer darstellbar ist, und a so gewählt, dass der Algorithmus spezielle Periodizitätseigenschaften besitzt. Die Implementierung der Berechnung der Reste bei der Division durch m wurde in Integer-Arithmetik realisiert. Letzterer Generator mit dem Namen „Minimal Standard“ wurde 1969 für das IBM System/360 entwickelt und hat sich im Laufe der Zeit weit verbreitet und ist immer noch in Verwendung. Der Primzahl-Modul hat wesentlichen Einfluss auf die Qualität der Verteilung der Zahlen des Generators.

RANDU

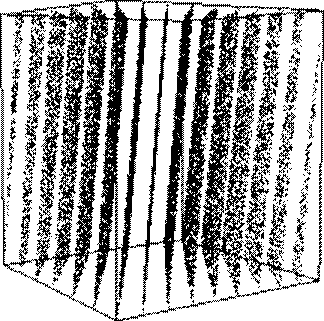
An dieser Stelle kommen wir zu einem wichtigen Ereignis in der Geschichte der Zufallszahlengeneratoren: Informatiker bei IBM haben Anfang der 70-iger Jahren versucht den Algorithmus effizienter zu implementieren. Dazu wurde als Modul an Stelle einer Primzahl die 2er Potenz m = 231 verwendet und der „Multiplikator“ a in der Nähe einer 2er Potenz, nämlich a=216+3 gewählt. Diese besondere Wahl ermöglicht es die Erzeugung der Zahlenfolge durch Shift-Operationen wesentlich zu beschleunigen. Dieser Generator mit dem Namen RANDU wurde zwar anfänglich getestet, man hat aber eine wichtige Fehlerquelle übersehen. Teilt man die Folge von RANDU Zufallszahlen in 3er Blöcke (u1, u2, u3), (u4, u5, u6), (u7, u8, u9), ... , dann liegen die dadurch entstandenen Punkte (x, y, z) nicht wie erwartet zufällig verteilt in einem 3-dimensionalen Quader sondern sie weisen eine sehr auffällige regelmäßige Struktur auf und liegen auf nur 15 Ebenen verteilt (siehe Bild). Dies bedeutet, dass man bei Verwendung von RANDU in drei-dimensionalen Simulationen völlig falsche Resultate erhalten würde. RANDU war ebenfalls wie der Minimal Standard Generator weit verbreitet. Diese geometrische Eigenschaft von RANDU lässt sich mathematisch nachweisen. Der Grund für diese 15 Ebenen liegt im Multiplikator 216+3. Würde man z.B. nur den Modul in eine Primzahl wie m=231-1 ändern, ergäbe sich eine ähnlich schlechte Struktur. Der 2er Potenz Modul bei RANDU hat zusätzlichen negativen Einfluss. Und zwar wird durch diesen Modul die Verteilung der Bits der einzelnen Zufallszahlen sehr regelmäßig. Dies kann bei falscher Transformation der Zufallszahlen zu erheblichen Fehlern in Simulationen führen.

Einen positiven Effekt hatte die Erkenntnis über die Schwächen von RANDU. Der Lehmer Algorithmus wurde genauestens untersucht. Man entwickelte schnelle und theoretisch und praktisch sehr genau analysierte Zufallszahlengeneratoren basierend auf verschiedensten arithmetischen Verfahren. Weiters wurden spezielle Zufallszahlen-Verfahren für die Anwendung bei Verschlüsselungstechnologien entwickelt.

Trotzdem sollte man aus dieser Geschichte zwei wichtige Dinge lernen. Es ist nicht immer vorrangig, „effizienter und schneller“ zu sein. Die Anwendung von Algorithmen in der Informatik gehört wohlüberlegt und analysiert, bevor Implementierungen verwendet werden. Dazu ist ein fundiertes Grundlagenwissen notwendig. D.H. Lehmer hat durch seine Erfahrung in der Zahlentheorie sehr wohl über das Verhalten seiner Methode bescheid gewusst. Nur kam es in Folge der Verbreitung dieser Idee zu den Fehlern, und ähnliches passiert in unserer schnelllebigen „Cut and Paste“ Zeit sicherlich auch in vielen anderen Bereichen der Informatik auch.

InfoBox1: Weitere historische Methoden der Zufallszahlengenerierung

Beispiele für Tabellen mit Zufallszahlen:

  • 1927: Tabelle mit 40.000 „zufälligen Bits, von L.H.C.Tippett. Ursprung: „Volkszählungsdaten“.
  • 1939: Mechanische Methoden („Roulett“) Bsp: Kendall, Babington-Smith: Tabelle mit 100.000 Zufalls-Bits.
  • 1955: „A Million Random Digits“ inkl. 100.000 normalverteilter Zahlen, RAND Corp. („Elektronisches Roulett“ als Basis)

Beispiel einer weiteren „arithmetischen“ Methode: die „Mid-square Method“:

Start = 6721 (beliebig)

(6721)2 = 45171841; zahl1=0.1718

(1718)2 = 29515240; zahl2=0.5152

(5152)2 = 26543204; zahl3=0.5432

...

Diese Methode wurde von dem berühmten Wissenschafter John Von Neumann vorgeschlagen. Von ihm stammt auch das Zitat: “Any one who considers arithmetical methods of producing Random Numbers is, of course, in a state of sin…”

Es lässt sich vermuten, dass diese Aussage aus der Erkenntnis resultiert, dass obige Methode sehr leicht zu sehr “schlechten Zufallszahlen“ führen kann.

InfoBox2: ENIAC - Electronic Numeric Integrator and Calculator

(US. Army Image)

Eckdaten: Entwicklung ab 1943; erster Start Jänner 1946; in Betrieb bis 1955; 18000 Röhren; 1500 Relais; 233 m2 Bodenfläche; 140 kW Energieverbrauch; 30t Gewicht; 20 Speicherplätze; rechnet mit (10) Bit Dezimalzahlen; 10.000.000 $ Kosten; Röhrenausfall alle paar Minuten;

http://www.science.uva.nl/faculteit/museum/eniacbox.html : ''In the beginning the ENIAC had only 20 memory locations, meant for input and output data and intermediate results, represented by 10-digits decimal numbers. In the original design programming was done using flip switches and patch cables (like in an old-fashioned telephone exchange). Von Neumann's stored-program concept was implemented during 1946: the machine's memory (which was extended in the meantime) was used since then for storing coded programs and subroutines as well.

The first applications were for the Manhattan hydrogen-bomb project. For the solution of a certain differential equation, 8 million multiplications and a comparable number of additions were needed. This took 15 system- hours, 20% of the time being used for test-runs. Nevertheless computing was done more than 1000 times faster than was possible with any equipment available then''

InfoBox3: D.H.Lehmer 1949 Zufallszahlengenerierung

Beispiel: Lehmer Algorithmus mit „Modul“ m = 108+1 und „Multiplikator“ a=23. Die Folge der ersten Zahlen lautet:

x2 = 232 = 529

x3 = 233 = 12167

.

x5 = 235 = 6436343

x6 = 236 = 148035889

Die Zahl x6 ist größer als der Modul m = 100000001 und wird somit durch den Rest bei Division durch m ersetzt, d.h. x6 = 48035888. Dieser Prozess wird für alle weiteren Zahlen x7, x8, ... fortgesetzt womit man eine Folge von ganzen Zahlen kleiner m erhält. Eine anschließende weitere Division durch den Modul m liefert die „normierten“ Zufallszahlen

u6=0.4804, u7=0.0483, u8=0.1098, ....

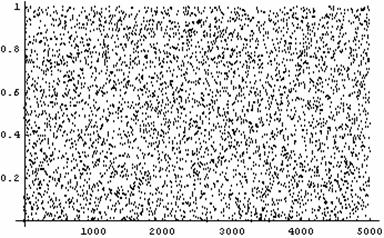
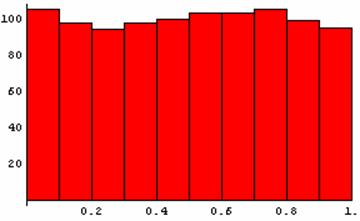
Die folgende Graphik visualisiert das Verhalten der ersten 5000 Zahlen dieses Algorithmus. Die Graphik daneben zeigt die gleichmäßige Verteilung der ersten 1000 Zahlen (jedes Intervall der Länge 1/10 enthält ungefähr 100 Zahlen).

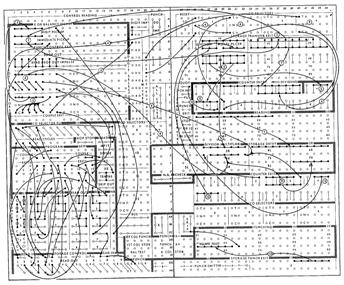
InfoBox4: IBM602A

http://www.users.nwark.com/~rcmahq/jclark/ibm602.htm : ''The IBM 602 Calculating Punch reads factors punched in IBM cards and performs mathematical operations of addition, subtraction, multiplication and division. The results of these calculations can then be punched into the same cards from which the factors were read or into trailer cards.

The standard machine can multiply a 22-digit multiplican by an 8-digit multiplier to obtain a 30 digit product. A 15-digit dividend can be divided by an 8-digit divisor to obtain and punch an 8-digit quotient. All operations of the 602 are performed in steps or operating cycles which occur at the rate of 200 per minute or 12,000 per hour. The number of cycles required for a card depends on the size of the factors and the type of problem. A glance at the picture will show the card path through the 602 is not straight, but the card actually makes a right angle turn. The operations of the 602 are controlled by wiring the control panel which is inserted into the front of the machine. Below is the wiring diagram to do square root.''

InfoBox5: Links

Der Autor bedankt sich für die Hilfestellung durch das Archiv der Bankroft Library der Universität von Kalifornien, Berkeley.